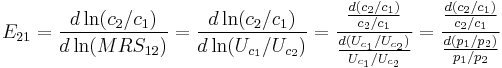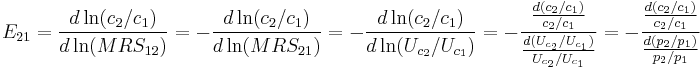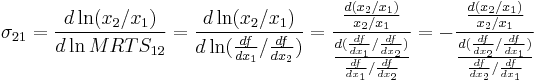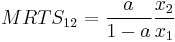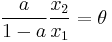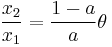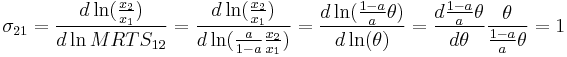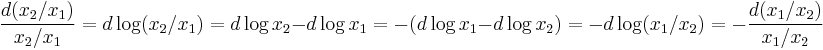Elasticity of substitution

Elasticity of substitution is the elasticity of the ratio of two inputs to a production (or utility) function with respect to the ratio of their marginal products (or utilities).[1] It measures the curvature of an isoquant and thus, the substitutability between inputs (or goods), i.e. how easy it is to substitute one input (or good) for the other.

Contents

Mathematical definition

Let the utility over consumption be given by 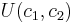U(c_1,c_2). Then the elasticity of substitution is:

E_{21} =\frac{d \ln (c_2/c_1) }{d \ln (MRS_{12})} =\frac{d \ln (c_2/c_1) }{d \ln (U_{c_1}/U_{c_2})} =\frac{\frac{d (c_2/c_1) }{c_2/c_1}}{\frac{d (U_{c_1}/U_{c_2})}{U_{c_1}/U_{c_2}}} =\frac{\frac{d (c_2/c_1) }{c_2/c_1}}{\frac{d (p_1/p_2)}{p_1/p_2}}

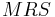where MRS is the marginal rate of substitution. The last equality presents 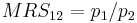MRS_{12} = p_1/p_2 which is a relationship from the first order condition for a consumer utility maximization problem. Intuitively we are looking at how a consumer's relative choices over consumption items changes as their relative prices change.

Alternatively:[2]

E_{21} =\frac{d \ln (c_2/c_1) }{d \ln (MRS_{12})} =-\frac{d \ln (c_2/c_1) }{d \ln (MRS_{21})} =-\frac{d \ln (c_2/c_1) }{d \ln (U_{c_2}/U_{c_1})} =-\frac{\frac{d (c_2/c_1) }{c_2/c_1}}{\frac{d (U_{c_2}/U_{c_1})}{U_{c_2}/U_{c_1}}} =-\frac{\frac{d (c_2/c_1) }{c_2/c_1}}{\frac{d (p_2/p_1)}{p_2/p_1}}

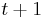In discrete-time models, the elasticity of substitution of consumption in periods t and t%2B1 is known as elasticity of intertemporal substitution.

Similarly, if the production function is 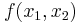f(x_1,x_2) then the elasticity of substitution is:

\sigma_{21} =\frac{d \ln (x_2/x_1) }{d \ln MRTS_{12}} =\frac{d \ln (x_2/x_1) }{d \ln (\frac{df}{dx_1}/\frac{df}{dx_2})} =\frac{\frac{d (x_2/x_1) }{x_2/x_1}}{\frac{d (\frac{df}{dx_1}/\frac{df}{dx_2})}{\frac{df}{dx_1}/\frac{df}{dx_2}}} =-\frac{\frac{d (x_2/x_1) }{x_2/x_1}}{\frac{d (\frac{df}{dx_2}/\frac{df}{dx_1})}{\frac{df}{dx_2}/\frac{df}{dx_1}}}

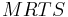where MRTS is the marginal rate of technical substitution.

The inverse of elasticity of substitution is elasticity of complementarity.

Example

Consider Cobb-Douglas production function 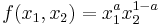f(x_1,x_2)=x_1^a x_2^{1-a}.

The marginal rate of technical substitution is

MRTS_{12} = \frac{a}{1-a} \frac{x_2}{x_1}

It is convenient to change the notations. Denote

\frac{a}{1-a} \frac{x_2}{x_1}=\theta

Rewriting this we have

\frac{x_2}{x_1} = \frac{1-a}{a}\theta

Then the elasticity of substitution is

\sigma_{21} = \frac{d \ln (\frac{x_2}{x_1}) }{d \ln MRTS_{12}} = \frac{d \ln (\frac{x_2}{x_1}) }{d \ln (\frac{a}{1-a} \frac{x_2}{x_1})} = \frac{d \ln (\frac{1-a}{a}\theta) }{d \ln (\theta)} = \frac{d \frac{1-a}{a}\theta}{d \theta} \frac{\theta}{\frac{1-a}{a}\theta}=1

Economic Interpretation

Given an original allocation/combination and a specific substitution on allocation/combination for the original one, the larger the magnitude of the elasticity of substitution (the marginal rate of substitution elasticity of the relative allocation) means the more likely to substitute. There are always 2 sides to the market; here we are talking about the receiver, since the elasticity of preference is that of the receiver.

Notes

  1. ^ Sydsaeter, Knut and Hammond, Peter, Mathematics for Economic Analysis, Prentice Hall, 1995, pages 561-562.
  2. ^ Given that:
    \ \frac{d (x_2/x_1)}{x_2/x_1} = d\log (x_2/x_1) = d\log x_2 - d\log x_1 = - (d\log x_1 - d\log x_2) = - d\log (x_1/x_2) = - \frac{d (x_1/x_2)}{x_1/x_2}
    an equivalent way to define the elasticity of substitution is:
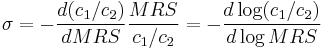    \ \sigma =-\frac{d (c_1/c_2)}{d MRS}\frac{MRS}{c_1/c_2}=-\frac{d\log (c_1/c_2)}{d\log MRS}.

See also

References

External links